Gemeine Brüche

Gebrochene Zahlen lassen sich als gemeine Brüche darstellen. Ein gemeiner Bruch ist eine Darstellung der Form

    \[\frac{a}{b}\]

Ein gemeiner Bruch bestehen aus

  • dem Bruchstrich
  • dem Zähler a (über dem Bruchstrich)
  • dem Nenner 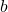b (unter dem Bruchstrich)

Dabei sind a und b natürliche Zahlen. Der Nenner ist die Zahl, die unter dem Bruchstrich steht. Der Nenner gibt an, in wie viele (gleich große) Teile das Ganze geteilt wurde. Die Zahl über dem Bruchstrich heißt Zähler. Der Zähler sagt dir, wie viele Teile ausgewählt wurden.

Beispiele für gemeine Brüche sind \frac{1}{4}, \frac{2}{3} oder \frac{5}{2}.

Aber was genau bedeutet nun zum Beispiel \frac{3}{4}?

Stell dir vor, du hast eine Pizza und du schneidest sie so, dass vier gleich große Teile entstehen. Diese Teile nennt man “Viertel”. Ein Teil gibst du einer anderen Person. Wie viel Pizza hast du dann noch? Nun, du hast mehr als 0, aber weniger als 1, denn von der ganzen Pizza fehlt ein Teil, genauer ein Viertel. Die Pizzamenge ist also keine natürliche Zahl. Aber du kannst sagen, dass du 3 Teile der Pizza hast, genauer drei Viertel. Und genau dafür benutzt man diese Bruchschreibweise: \frac{3}{4} bedeutet, wir haben ein Ganzes in vier gleich große Teile geteilt und davon drei Teile ausgewählt.

BEACHTE: Der Bruchstrich entspricht dabei dem Divisionszeichen, das heißt \frac{2}{3} ist eine Darstellungsform des Ergebnisses der Division 2 : 3. Eine andere Möglichkeit gebrochene Zahlen darzustellen, sind Dezimalzahlen.

Inhaltsübersicht

Echte und unechte Brüche und gemischte Zahlen

Brüche, deren Zähler kleiner ist als der Nenner, nennt man echte Brüche, die anderen nennt man unechte Brüche. So sind zum \frac{3}{4} und \frac{2}{7} echte Brüche. Dagegen sind \frac{11}{6} und \frac{5}{5} unechte Brüche, da ihre Zähler nicht kleiner sind als die Nenner.

Unechte Brüche sind immer größer gleich 1. Deshalb kannst du unechte Brüche auch als gemischte Zahlen schreiben, d. h. als eine natürliche Zahl zusammen mit einem echten Bruch. Zum Beispiel ist 13 : 5 = 2 Rest 3, denn 2 \cdot 5 + 3 = 10 + 3 = 13. Somit kannst du den unechten Bruch auch so schreiben:

    \[\frac{13}{5} = 2 \frac{3}{5}\]

Dabei ist 2 \frac{3}{5} eigentlich eine Kurzschreibweise für 2 + \frac{3}{5}.

Gemeine Brüche multiplizieren und dividieren

Für das Multiplizieren von gemeinen Brüchen gilt die einfache Regel: Zähler mal Zähler und Nenner mal Nenner

    \[\frac{2}{3} \cdot \frac{4}{7} = \frac{2 \cdot 4}{3 \cdot 7} = \frac{8}{21}\]

Den Kehrwert oder das Reziproke eines Bruchs \frac{a}{b} bildest du, indem du Zähler und Nenner vertauschst: \frac{b}{a}. Der Kehrwert von \frac{2}{7} ist also \frac{7}{2} (sprich “sieben Halbe”).

Für das Dividieren von gemeinen Brüchen gilt: Du dividierst durch einen gemeinen Bruch, indem du mit dessen Kehrwert multiplizierst.

    \[\frac{1}{5} : \frac{4}{3} = \frac{1}{5} \cdot \frac{3}{4} = \frac{1 \cdot 3}{5 \cdot 4} = \frac{3}{20}\]

Gemeine Brüche erweitern und kürzen

Einen gemeinen Bruch \frac{a}{b} mit einer natürlichen Zahl c \ne 0 erweitern heißt, Zähler und Nenner mit c zu multiplizieren.

    \[\frac{2}{5} \stackrel{\cdot 3}{=} \frac{2 \cdot 3}{5 \cdot 3} = \frac{6}{15}\]

Durch erweitern machst du Zahlen in Zähler und Nenner größer. Es gibt auch die umgekehrte Richtung: Einen gemeinen Bruch \frac{a}{b} mit einer natürlichen Zahl c \ne 0 kürzen bedeutet, Zähler und Nenner durch c zu dividieren. Beachte, dass dies nur möglich ist, wenn Zähler UND Nenner durch c teilbar sind!

    \[\frac{12}{8} \stackrel{: 4}{=} \frac{12 : 4}{8 : 4} = \frac{3}{2}\]

Beachte, dass sich der Wert eines Bruches durch Erweitern oder Kürzen NICHT ändert. Das heißt, \frac{2}{5} und \frac{6}{15} sind nur verschiedene Darstellungsweisen derselben Zahl. Verschiedene gemeine Brüche, die dieselbe Zahl darstellen nennt man gleichwertig.

Gleichnamige Brüche

Gleichnamige Brüche erkennen

Gemeine Brüche, die den gleichen Nenner haben heißen gleichnamig, andernfalls nennt man sie ungleichnamig.

\frac{4}{6} und \frac{11}{6} sind also gleichnamig, da beide Brüche den Nenner 6 haben. \frac{3}{4} und \frac{8}{5} sind also ungleichnamig, da sie verschiedene Nenner haben.

Warum sind gleichnamigen Brüche so wichtig?

Nun, wenn Brüche gleichnamig sind, heißt das, dass bei ihnen das Ganze jeweils in gleich viele Teile geteilt wurde. Das ist sehr hilfreich sowohl beim Vergleichen als auch beim Addieren und Subtrahieren.

Gemeine Brüche gleichnamig machen

Zwei Brüche gleichnamig machen bedeutet, die Brüche durch erweitern oder kürzen so umzuformen, dass sie den gleichen Nenner haben. Idealerweise sucht man den sog. Hauptnenner. Der Hauptnenner ist der kleinste gemeinsame Nenner, auf die sich die Brüche durch Erweitern oder Kürzen bringen kann. Man unterscheidet zwei Fälle

Fall 1: Ein Nenner ist ein Vielfaches des anderen Nenners

Beispiel: \frac{2}{7} und \frac{6}{14}. 14 ist ein Vielfaches von 7, denn 7 \cdot 2 = 14. Du brauchst also nur den linken Bruch mit 2 erweitern

    \[\frac{2}{7} \stackrel{\cdot 2}{=} \frac{4}{14}\]

und schon haben beide Brüche den gleichen Nenner, sind also gleichnamig.

Fall 2: Allgemeiner Fall (kein Nenner ist ein Vielfaches des anderen Nenners)

Im allgemeinen Fall gilt: Sind die Brüche voll gekürzt, dann ist der Hauptnenner das kleinste gemeinsame Vielfache (kgV) der Nenner.

Beispiel: \frac{4}{5} und \frac{3}{2}. Keiner der beiden Nenner ist ein Vielfaches des anderen. Beide Brüche sind voll gekürzt. Der Hauptnenner ist also das kleinste gemeinsame Vielfache von 5 und 2. Betrachten wir als die Vielfachen der beiden Nenner:

2, 4, 6, 8, \mathbf{10}, 12, 14, 16, 18, \mathbf{20}, 22, ...
5, \mathbf{10}, 15, \mathbf{20}, 25, ...

Das heißt zum Beispiel sind 10 und 20 gemeinsame Vielfache von 2 und 5. Da kleinste der gemeinsamen Vielfachen ist 10. Um die Brüche gleichnamig zu machen, erweitern wir beide Brüche als 10-tel:

    \[\frac{4}{5} \stackrel{\cdot 2}{=} \frac{8}{10} \qquad \frac{3}{2} \stackrel{\cdot 5}{=} \frac{15}{10}\]

Gemeine Brüche vergleichen

Bei gemeinen Brüchen gibt der Nenner an, in wie viele (gleich große) Teile das Ganze geteilt wurde, und der Zähler sagt uns, wie viele Teile davon ausgewählt wurden. Dennoch fällt es uns schwer, auf Anhieb zu sagen, welcher der beiden Brüche \frac{5}{8} und \frac{7}{12} größer ist. Gemeine Brüche kannst du gut vergleichen, wenn entweder die Zähler oder die Nenner gleich sind. Schau dir hierzu die folgenden drei Fälle an.

1. Fall: Gleichnamige Brüche vergleichen

Besonders einfach ist der Fall, wenn die Brüche gleichnamig sind. In diesem Fall gilt:

Sind zwei gemeine Brüche gleichnamig, so ist der Bruch größer, dessen Zähler größer ist.

Für \frac{5}{11} und \frac{9}{11} gilt \frac{5}{11} < \frac{9}{11}, weil 5 < 9 ist.

2. Fall: Ungleichnamige Brüche vergleichen

Wie sieht es nun in unserem Beispiel von oben aus: \frac{5}{8} und \frac{7}{12}? Nun, in diesem Fall müssen wir zuerst beide Brüche gleichnamig machen. Dann ist der Vergleich – wie im 1. Fall gesehen – recht einfach:

Du machst die beiden also zunächst durch Erweitern gleichnamig: \frac{5}{8} \stackrel{\cdot 3}{=} \frac{15}{24} und \frac{7}{12} \stackrel{\cdot 2}{=} \frac{14}{24}. Nun vergleichst du die Zähler. Und wegen 15 > 14 gilt schließlich \frac{5}{8} > \frac{7}{12}.

3. Fall: Brüche mit gleichem Zähler vergleichen

Genauso einfach wie im 1. Fall ist die Situation, wenn die Brüche die gleichen Zähler haben. Dann gilt

Haben zwei Brüche den gleichen Zähler, so ist der Bruch größer, dessen Nenner kleiner ist.

Beispiel: Vergleiche \frac{8}{13} und \frac{8}{9}. Wegen 9 < 13 gilt \frac{8}{13} < \frac{8}{9}.

Gemeine Brüche addieren und subtrahieren

Nehmen wir an, du hast folgende Aufgabe: \frac{1}{2} + \frac{2}{3}.

ACHTUNG: Auf keinen Fall darfst du einfach die Zähler und die Nenner addieren! Denn gemeine Brüche lassen sich nur addieren/subtrahieren, wenn sie gleichnamig sind. Deshalb unterscheiden wir zwei Fälle.

1. Fall: Gleichnamige Brüche addieren/subtrahieren

Sind zwei Brüche gleichnamig, so ist der Fall recht einfach.

Du addierst/subtrahierst zwei gleichnamige Brüche, indem du die Zähler addierst/subtrahierst und den (gemeinsamen) Nenner beibehältst.

Beispiel: \frac{3}{8} + \frac{7}{8}

Die Brüche sind gleichnamig, da bei den Nenner 8 haben. Also addierst du die Zähler und behältst den Nenner bei:

    \[\frac{3}{8} + \frac{7}{8} = \frac{3+7}{8} = \frac{10}{8}\]

2. Fall: Ungleichnamige Brüche addieren/subtrahieren

Wie sieht es nun mit unserem Beispiel von oben aus: \frac{1}{2} + \frac{2}{3}?

Die beiden Brüche sind ungleichnamig. Nun kombinierst du zwei Dinge, die schon kennst: 1) du kannst ungleichnamige Brüche gleichnamig machen und 2) du kannst gleichnamige Brüche addieren (siehe 1. Fall).

Also machst du zunächst die beiden Brüche gleichnamig: \frac{1}{2} \stackrel{\cdot 3}{=} \frac{3}{6} und \frac{2}{3} \stackrel{\cdot 2}{=} \frac{4}{6}. Nun kannst du die gleichnamigen Brüche wie im Fall 1 addieren:

    \[\frac{1}{2} + \frac{2}{3} = \frac{3}{6} + \frac{4}{6} = \frac{3+4}{6} = \frac{7}{6}\]

Gemeine Brüche in Dezimalzahlen umwandeln

Bisher haben wir gemeine Brüche betrachtet. Es gibt auch noch eine weitere Möglichkeit, gebrochene Zahlen darzustellen, nämlich als Dezimalzahlen. Dezimalzahlen sind Zahlen in Kommaschreibweise. Sicher kennst du die Schreibweise der natürlichen Zahlen mit Einer (10^0), Zehner (10^1), Hunderter (10^2) usw. Dies lässt nach rechts fortsetzen mit Zehntel (10^{-1}), Hundertstel (10^{-2}), Tausendstel (10^{-3}) usw. Zwischen Einer und Zehntel setzt man ein Komma, um den Übergang deutlich zu machen. Hier ein Beispiel:

    \[427{,}956\]

Deshalb stellt sich die Frage, wie wandelt man einen gemeinen Bruch in die entsprechende Darstellung als Dezimalzahl um?

Fall 1: Zehnerbrüche in Dezimalzahlen umwandeln

Brüche, deren Nenner Zehnerpotenzen sind (also 10, 100, 1000 usw.), nennt man Zehnerbrüche. Solche Zehnerbrüche lassen sich leicht in Dezimalzahlen umwandeln. Betrachte zum Beispiel

    \[\frac{27}{100}\]

Die Regel ist einfach:

Du schaust, wie viele Nullen der Nenner hat. So viele Stellen gehst du nach links und setzt dort das Komma.

Für unser Beispiel gilt:

    \[\frac{27}{100} = 0{,}27\]

Von der 27 aus gehst du zwei Stellen nach links und setzt dort das Komma. Wenn links vom Komma nichts steht, schreibst du dort eine Null hin.

Freie Stellen werden mit Nullen aufgefüllt. So zum Beispiel bei

    \[\frac{5}{1000} = 0{,}005\]

Hier gehst du von der 5 aus drei Stellen nach links, da die 1000 drei Nullen hat.

Im folgenden Beispiel hat der Nenner eine Null. Du gehst also eine Stelle nach links und setzt dort das Komma:

    \[\frac{294}{10} = 29{,}4\]

Fall 2: Brüche, die sich in Zehnerbrüche umformen lassen, in Dezimalzahlen umwandeln

Wie sieht es aber zum Beispiel mit \frac{12}{25} aus?

Nun, dies ist zwar kein Zehnerbruch, da der Nenner keine Zehnerpotenz ist. Aber der Bruch lässt sich durch Erweitern in einen Zehnerbruch umformen und dann wie in Fall 1 als Dezimalzahl schreiben:

    \[\frac{12}{25} \stackrel{\cdot 4}{=} \frac{48}{100} = 0{,}48\]

Fall 3: Brüche, die sich nicht in Zehnerbrüche umformen lassen, in Dezimalzahlen umwandeln

Der dritte Fall sind Brüche, die keine Zehnerbrüche sind und sich auch nicht in solche umformen lassen, wie zum Beispiel \frac{4}{11}.

Um solche gemeinen Brüche in Dezimalzahlen umzuwandeln, musst du die schriftliche Division ausführen:

    \[4 : 11 = 0{,}3636... = 0{,}\overline{36}\]

Spricht: “null Komma drei sechs Periode drei sechs”. Man nennt solche Brüche, bei denen sich eine bestimmte Ziffernfolge wiederholt periodisch. Man schreibt die Periode nur einmal und setzt einen Strich darüber.

Abbrechende und periodische Dezimalzahlen

MERKE: Wenn du einen gemeinen Bruch in einen Dezimalbruch umwandelst, erhältst du immer eine Dezimalzahl, die entweder abbrechend/endlich oder periodisch ist.

Eine Dezimalzahl heißt endlich oder abbrechend, wenn die Anzahl der (von null verschiedenen) Nachkommastellen endlich ist. Zum Beispiel gilt: \frac{3}{4} = 0{,}75.

Die Brüche in Fall 3 führen auf periodische Dezimalzahlen. Eine Dezimalzahl nennt man periodisch, wenn die Anzahl der Nachkommastellen unendlich ist und sich nach einer endlichen Anzahl von Nachkommastellen ein bestimmte Ziffernfolge – “Periode” genannt – wiederholt. Beginnt die Periode direkt nach dem Komma wie bei 0{,}\overline{45} nennt man die Zahl reinperiodisch. Beginnt die Periode erst später wie bei 0{,}6\overline{81} spricht man von gemischt-periodisch. Die Ziffern vor der Periode nennt man Vorziffern oder Vorperiode.

Negative gemeine Brüche

Bisher waren Zähler und Nenner natürliche Zahlen, also positiv. Was ist nun, wenn Zähler oder Nenner negativ sind?

Ganz oben hatten wir gesagt, dass der Bruchstrich dem Divisionszeichen entspricht. das heißt der gemeine Bruch \frac{3}{4} ist eine Darstellungsform des Ergebnisses der Divisionsaufgabe 3 : 4. Für das Multiplizieren und Dividieren mit ganzen Zahlen gilt außerdem, das gleiche Vorzeichen plus und ungleiche Vorzeichen minus ergeben:

  • + mal + ergibt +
  • – mal – ergibt +
  • + mal – ergibt –
  • – mal + ergibt –

Und für “durch” statt “mal” gilt das Gleiche. Zusammen bedeutet das: Haben Zähler und Nenner das gleich Vorzeichen, ist der ganze Bruch positiv. Haben Zähler und Nenner hingegen ungleiche Vorzeichen, ist der gesamte Bruch negativ. Du schreibst das Vorzeichen, dann vor den Bruchstrich. Es gilt also

    \[\frac{(-3)}{5} = \frac{3}{(-5)} = -\frac{3}{5}\]

Hast du umgekehrt einen negativen Bruch vor dir, dann ist beim Addieren und Subtrahieren sinnvoll, das Minus dem Zähler zuzuordnen. Denn der Nenner gibt an, in wie viele Teile das Ganze geteilt wurde, aber die Zähler zählen die Anzahl der ausgewählten Teile. Hier ein Beispiel:

    \[-\frac{1}{3} + \frac{1}{2} = -\frac{1 \cdot 2}{3 \cdot 2} + \frac{1 \cdot 3}{2 \cdot 3} = -\frac{2}{6} + \frac{3}{6} = \frac{(-2)}{6} + \frac{3}{6} = \frac{(-2)+3}{6} = \frac{1}{6}\]